日前,我院夏勇教授👩🏼🦳、2015级博士生杨美佳、2014级博士生王姝,在凸几何计算领域取得重要进展🛍。研究成果“Chebyshev Center of theIntersection of Balls: Complexity, Relaxation and Approximation”在国际期刊《Mathematical Programming》在线发表🗑,该期刊为数学优化领域知名期刊🪿,2018年影响因子为3.785🌾。(论文链接👂🏽:)
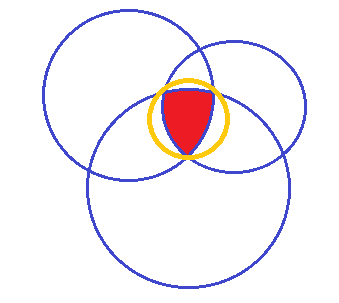
该问题可追溯到英国著名数学家👮🏿♀️、皇家学会会员Sylvester,他于1857年提出平面上有限多个点的最小圆覆盖问题✂️👷🏻♂️,即寻找这有限个点的切比雪夫中心🙆🏿♂️🛋,推而广之的问题是对一些凸集寻找其切比雪夫中心。寻找n维空间p个球的交集的切比雪夫中心问题由著名优化专家、FISTA提出者🧽、以色列理工凯发K8Beck教授2007年提出🚵🏿,在鲁棒估计、无线网络通信👳🏿、控制🌠🤸🏼♂️、优化等领域有重要应用🧑🏻🦽➡️。如下图示为一个n=2,p=3的例子⬅️,黄色圆为覆盖红色区域的最小圆👨🏽🦲。
Beck教授2007年通过对偶松弛提出该问题的标准二次规划近似方法💇🏿♂️,并证明当p≤n-1时,该近似是精确的⚄。2009年Beck教授将该充分条件进一步放松成p≤n🧛🏼♀️。
夏勇教授课题组对该问题进行了深入的研究,并取得了重要成果💁🏼♀️。证明了该问题是NP-hard✷😓;首次理论分析了p>n的情形☑️,证明了p-n固定或者n固定时🌘,该问题是多项式可解👩🏻🦼➡️;此外,首次证明了Beck教授建立的标准二次规划近似方法存在一个渐近为2的近似比(近似比为2意指近似解的函数值不超过精确最小值的2倍)🧑🦼。
该项工作得到国家自然科学基金优秀青年科学基金、面上项目🔴、青年基金资助,也得到北京市自然科学基金重点项目资助。

